Topographic Locally Competitive Algorithm
Recent studies have shown that, in addition to the emergence of receptive fields similar to those observed in biological vision using sparse representation models, the self organization of said receptive fields can emerge from group sparsity constraints. Here I will briefly review research demonstrating topological organization of receptive fields using group sparsity principles and then describe a two-layer model implemented in a Locally Comptetitive Algorithm that will be termed Topographical Locally Competitive Algorithm (tLCA).
Topographic Organization of Receptive Fields
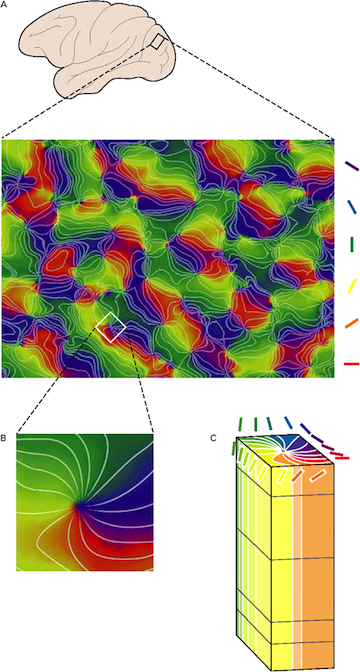
In biological vision, receptive fields in early visual cortex are organized into orientation columns where adjacent columns have selectivity close in feature space. The global appearance of selectivity to oreintation across the coritical sheet is that of smooth transitions between orientation preference of columns and the classic pinwheel features where orientation column selectivities meet at a singularity (see image below).
A large amount of computational research has explored the mechanisms underlying such organization (Swindale, 1996). More recent research has learned the self-organization of feature detectors based on the natural statistics of images when structured sparsity is imposed (Hyvärinen, Hoyer, & Inki, 2001; Jia & Karayev, 2010; Kavukcuoglu, Ranzato, Fergus, & Le-Cun, 2009; Welling, Osindero, & Hinton, 2002).1 Most of these models involve a two layers where the activations of the first layer are square rectified and projected up to a second layer based on locally defined connections. If we have activations in the first layer given by:
\begin{equation} a^{(1)} = \mathbf{w}^T \mathbf{x} \end{equation}
where is the weight matrix and is the input data, these can then be projected up to a second layer unit given the local connections defined by overlapping neighborhoods :
\begin{equation} a_i^{(2)} = \sqrt{\sum_{j \in H_i} (a^{(1)}_j)^2 } \end{equation}
Thus, the activation of each unit in the second level is the sum of sqares of adjacent units in the first layer as defined by a local connectivity matrix that can either be binary or have some distribution across the nieghborhood (below is an example of 3 X 3 overlapping neighborhoods).

An example showing 3x3 overlapping neighborhoods
To avoid edge artifacts, these neighborhoods are also commonly defined to be toroidal so that each unit in a given layer has an equal number of neighbors.
Thus the optimization objective for a sparse-penalized least-squares reconstruction model with the aforementioned architecture would be:
\begin{equation} \min_{\mathbf{\alpha}\in\mathbb{R}^m} \vert\vert \mathbf{x} - \mathbf{w}^T a^{(1)} \vert\vert^2_2+\lambda\vert\vert a^{(1)} +a^{(2)} \vert\vert_1 \end{equation}
where, as before, is a sparsity tradeoff parameter.
Self-Organization of Receptive Fields using Locally Competitive Algorithms
Locally Competitive Algorithm
Locally competitive algorithms (Rozell, Johnson, Baraniuk, & Olshausen, 2007) are dynamic models that are implementable in hardware and converge to good solutions for sparse approximation. In these models, each unit has an state , and when presented with a stimulus , each unit begins accumulating activity that leaks out over time (much like a bucket with small holes on the bottom). When units reach a threshold , they begin exerting inhibition over their competitors weighted by some function based on similarity or proximity in space. The states of a given unit is represented by the nonlinear ordinary differential equaion
where represents increased activation proportional to the receptive field’s similarity to the incoming input. The internal states of each unit and thus the degree of inhibition that they can exert are expressed by a hard thresholding function which simply means that if the state of a unit is below the threshold, its internal state is zero, and if the state is above threshold, it’s internal state is a linear function of . This inhibition is finally wieghted based on the similarity between two units ensuring that redundant feature representations are not used for any given input and a sparse approximation is achieved.
A simple implementation of LCA in MATLAB is as follows (more details given later in post):
1 function [a] = LCA(W, X, neurons, batch_size, thresh)
2
3 % get activation values (b) and similarity values (G)
4 b = W' * X; % [neurons X examples]
5 G = W'* W - eye(neurons); % [neurons X neurons]
6
7 % LCA
8 u = zeros(neurons,batch_size); % unit states
9 for l =1:10
10 a = u .* (abs(u) > thresh); % internal activations
11 u = 0.9 * u + 0.01 * (b - G * a); % update unit states
12 end
13 a = u .* (abs(u) > thresh); % [groups, batch_size]The distribution of activation across both the population and examples is very sparsely distributed, with most activation values at zero, and only very few greater-than-zero values.
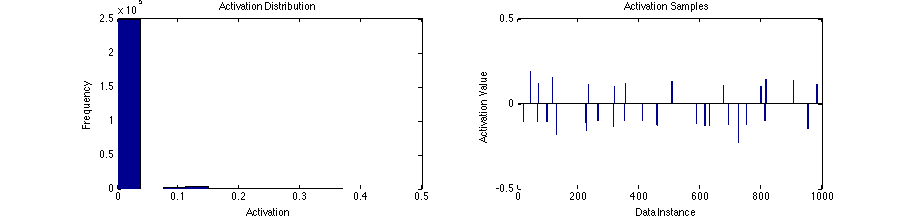
Activation distribution and sample for LCA
Observing the weights that are learned, we can also see that, consistent with previous research, LCA learns Gabor-like receptive fields.

Receptive fields learned using LCA
It is also interesting to consider the reconstruction performance of the learned receptive fields.

Left: original image; Right: reconstructed image
The reconstructed image clearly captures the most important structural features of the original image and removes much of the noise.
tLCA Model
Here I will introduce a two-layer Locally Competitive Algorithm that I will call Topographical Locally Competitive Algorithm (tLCA). The general procedure is to first determine the initial activity of the first layer, immediately project it to the second layer in a fast feedforward manner, perform LCA at the second layer, project the activity back down to the first layer, and then perform LCA on the first layer (see figure for schematic illustration).
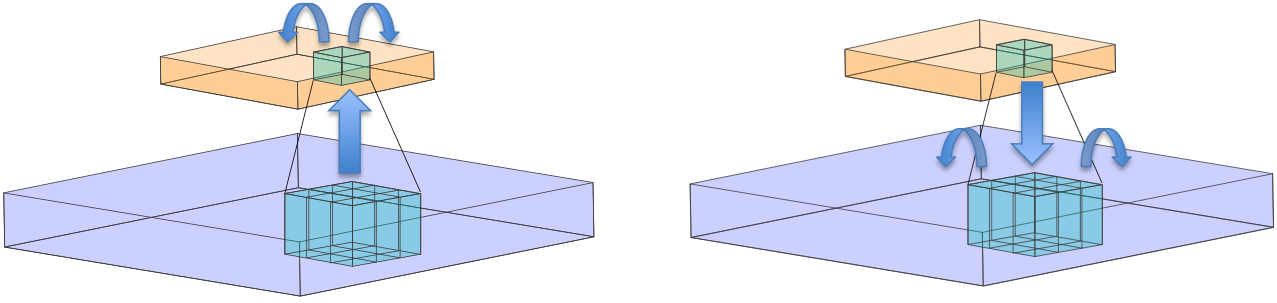
Illustration of the network architecture and procedure. The activation for the first layer (blue) is calculated and then local connections from the second layer (orange) to the first allow for it to pool over a neighborhood of units (cyan). Local competition is then performed on the second layer. In the right panel, after LCA on the second layer terminates, activations are then projected back down to the first layer via local connections. Finally LCA on the first layer is conducted until termination.
Now we will walk through the steps of bulding the model (to see all code navigate to my tLCA repository). To begin building the model, we will first define some parameters:
1 % set environment parameters
2 neurons = 121; % number of neurons
3 patch_size = 256; % patch size
4 batch_size = 1000; % batch size
5 thresh = 0.1; % LCA threshold
6 h = .005; % learning rate
7 blocksize = 3; % neighborhood size
8 maxIter = 1000; % maximum number of iterationsWe can then randomly initialize the wieghts of the network and constrain them to lie on the ball via normalization:
1 W = randn(patch_size, neurons); % randomly initialize wieghts
2 W = W * diag(1 ./ sqrt(sum(W .^ 2, 1))); % normalize the weightsNext we need to define the local connectivities between the first layer and the second layer. These weights are held constant and are not trained like the weights of the first layer that connect to the input. To do so, we define a function gridGenerator with arguments neurons and filterSize and returns a group x neurons matrix blockMaster that contains binary row vectors with filled entries corresponding to neurons that belong to the group.
1 function blockMaster = gridGenerator(neurons, filterSize)
2
3 % determine grid dimensions
4 gridSize = sqrt(neurons);
5
6 % create matrix with grids
7 blockMaster = zeros(neurons, neurons);
8 c = 1;
9 x = zeros(gridSize, gridSize);
10 x(end - (filterSize - 1):end, end - (filterSize - 1):end) = 1;
11 x = circshift(x, [1, 1]);
12 for i = 1:gridSize
13 for j = 1:gridSize
14 temp = circshift(x, [i, j]);
15 blockMaster(c,:) = temp(:)';
16 c = c + 1;
17 end
18 endThis works by first creating a binary matrix with ones over the group centered at x(1,1) (lines 9 - 11); because it is toriodal, there are ones on opposite sides of the matrix. Then, for all groups, it shifts this primary matrix around until all group local connections have been created and saved into the master matrix.
Now that we have a means of projecting the first layer activation up to the second layer, we need to define how inhibition between units in the second layer should be weighted. We can define the mutual inhibiiton between two units in the second layer as being proportional to how many units in the first layer share their local connections. This can be conveniently created as follows:
1 % create group inhibition weight matrix
2 G2 = blockMaster * blockMaster';
3 G2 = G2 ./ max(max(G2));
4 G2 = G2 - eye(neurons);Lastly we need to also set up a similarity matrix for all pairwise connections between units. In the traditional LCA, this was computed as the similarity between receptive fields as described previously. Here we instead compute similarity as Euclidean distance in simulated cortical space. We can compute the distance of each unit to all other units using the function lateral_connection_generator:
1 function master = lateral_connection_generator(neurons)
2
3 % define grid size
4 dim = sqrt(neurons);
5
6 % create list of all pairwise x-y coordinates
7 x = zeros(dim * dim, 2);
8 c = 1;
9 for i = 1:dim
10 for j = 1:dim
11 x(c, :) = [i, j];
12 c = c + 1;
13 end
14 end
15
16 % create distance matrix of each cell from the center of the matrix
17 center_index = ceil(neurons / 2);
18 center = x(center_index, :);
19 temp = zeros(dim, 1);
20 for j = 1:size(x, 1)
21 temp(j) = norm(center - x(j, :));
22 end
23 temp = reshape(temp, [dim, dim]);
24
25 % shift the center of the matrix (zero distance) to the bottom right corner
26 temp = circshift(temp, [center_index - 1, center_index - 1]);
27
28 % create master matrix
29 master = zeros(neurons, neurons);
30 c = 1;
31 for i = 1:dim
32 for j = 1:dim
33 new = circshift(temp, [j, i]);
34 master(c, :) = new(:)';
35 c = c + 1;
36 end
37 endNow we are ready to actually run the neural network and analyze its characteristics. Image patches that were preselected from natural images and preprocessed through normalization are read in and assigned to the variable X. Then we loop through each training iteration and perform the following procedure:
- Normalize the weights as a form of regularization (as done previously)
1 W = W * diag(1 ./ sqrt(sum(W .^ 2, 1))); % normalize the weights- Rapidly feed forward the activation through first and on to the second level
1 b1 = W' * X; % [neurons X examples]
2 b2 = (blockMaster * sqrt(b1 .^ 2)) / blocksize; % [groups X examples]- Perform LCA at layer 2
1 u2 = zeros(groups,batch_size);
2 for i = 1:5
3 a2 = u2 .* (abs(u2) > thresh);
4 u2 = 0.9 * u2 + 0.01 * (b2 - G2 * a2);
5 end
6 a2=u2.*(abs(u2) > thresh); % [groups, batch_size]- Project the activations back down to the first layer
1 a1 = blockMaster' * a2; % [neurons X batch_size]
2 a1 = a1 .* b1; % weight by first level activation- Perform LCA on the first layer
1 u1 = a1;
2 for l =1:10
3 a1=u1.*(abs(u1) > thresh);
4 u1 = 0.9 * u1 + 0.01 * (b1 - G1*a1);
5 end
6 a1=u1.*(abs(u1) > thresh); % [groups, batch_size]- Update the weights
1 W = W + h * ((X - W * a1) * a1');Running this code using maxIter as set above takes just over a minute. The features that are learned replicate those found in the literature and they also self organize as has been found in the studies cited. An important observation is that the receptive fields organize by both orientation and spatial frequency, whereas lateral connections alone (run latLCA.m for comparison) only leads to some organization of orientation. Therefore, performing LCA in a two-layer network as we did here seems to be necessary to get good self organization along both dimensions. It is also important to note that phase appears to organize randomly, and this is due to the square rectification of the first layer (i.e., a counter-phase stimulus may result in a negative activation, but this will be rectified into a positive activation).

tLCA receptive fields
The activation distributions of both the first and second level are very sparse, just as in regular LCA.

tLCA activation distributions for both levels
When we look at the activity distribution across cortical space for both levels of the network, we see that they are very localized. Also note that there is a high degree of overlap between activations across the two levels.
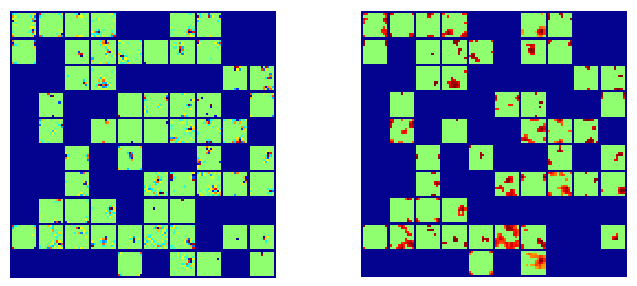
tLCA activation distributions across the first and second level of the hierarchy
We can also see that the reconstruction capability of tLCA is on par with LCA.

tLCA reconstruction. Left: original image; Right: reconstructed image
The reason for the poorer reconstruction performance is because of the smaller number of neurons, their more dependent activity, and fewer iterations in training.
References
- Antolı́k Ján, & Bednar, J. A. (2011). Development of maps of simple and complex cells in the primary visual cortex. Frontiers In Computational Neuroscience, 5.
- Hyvärinen, A., Hoyer, P., & Inki, M. (2001). Topographic independent component analysis. Neural Computation, 13(7), 1527–1558.
- Jia, Y., & Karayev, S. (2010). Self-Organizing Sparse Codes.
- Kavukcuoglu, K., Ranzato, M. A., Fergus, R., & Le-Cun, Y. (2009). Learning invariant features through topographic filter maps. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on (pp. 1605–1612). IEEE.
- Rozell, C., Johnson, D., Baraniuk, R., & Olshausen, B. (2007). Locally competitive algorithms for sparse approximation. In Image Processing, 2007. ICIP 2007. IEEE International Conference on (Vol. 4, pp. IV–169). IEEE.
- Swindale, N. V. (1996). The development of topography in the visual cortex: a review of models. Network: Computation In Neural Systems, 7(2), 161–247.
- Welling, M., Osindero, S., & Hinton, G. E. (2002). Learning sparse topographic representations with products of student-t distributions. In Advances in neural information processing systems (pp. 1359–1366).
-
Although these models have the advantage of being driven by natural image statistics, they also suffer from some biological implausibility (Antolı́k Ján & Bednar, 2011). ↩
Posted in Programming with tags: Sparse Coding, LCA, MATLAB